What are Fractals?

Disclaimer

With this post I am not trying to teach you everything about fractals, going into some heavy mathy theoretical aspects or anything of the sort, as I also don’t know that… that is way beyond the scope of my own knowledge as I am no expert my self. My objective with this post is to just talk briefly about fractals, laying some theoretical foundations before jumping into the actual fun part: drawing fractals with code.

What are fractals?

If you are reading this, chances are you’ve already come across some of the more famous fractal shapes around, like the Von Koch snowflake, the Sierpinski triangle and the Mandelbrot set, just to name a few.

So, what are they anyway? Well, there are 2 commonly accepted definitions for fractals, both created by Benoît Mandelbrot. When Mandelbrot coined the term fractals he firstly defined them in the following manner: “A fractal is by definition a set for which the Hausdorff–Besicovitch dimension strictly exceeds the topological dimension.” What did he mean by that? To understand this definition, we first need to understand what is a topological dimension and what is a Hausdorff dimension.

Topological Dimension and Hausdorff Dimension

In mathematics a topological dimension is a concept that measures the complexity of a space. It basically tells us in how many directions we can move around in a given space. For example, if we draw a dot on a table and put an object on top of it, now, if we were to try to move the object along the dot, there would be no direction to move it because the dot is a single point and has no width, height or depth, that is why we say the dot has 0 dimensions. But If we were to repeat the experiment, putting the object on top of a sheet of paper, we could now move our object in two directions: forwards-backwards and up-down (where diagonals are just the vector sum of those movements), which means that a sheet of paper has 2 dimensions (ignoring its thickness and treating it like a plain square). Ok, and what about the Hausdorff dimension? The Hausdorff dimension measures how “intricate”, how “detailed” a shape is.

Lets try our hand on some quick examples and calculate the Hausdorff dimensions for a regular square and for the Koch Curve fractal following that. We can do that by observing how many “copies of itself” a shape creates as it increases in length and applying a very simple formula often referred as the scaling law:

Where N is the number of smaller copies of the shape needed to fully cover the new shape, R is the magnifying factor (by how much we are extending our shape) and D is the dimension of the shape, lets try and apply it to our examples:

1. First we draw a regular 2 by 2 square:

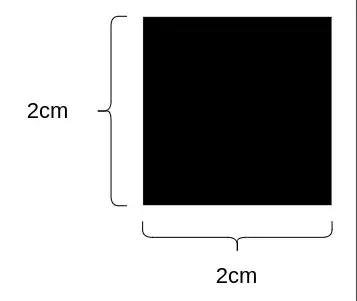
2. Now we extend the length of its base by 2 and, as we extend its base, we also have to extend its side, to keep proportions.

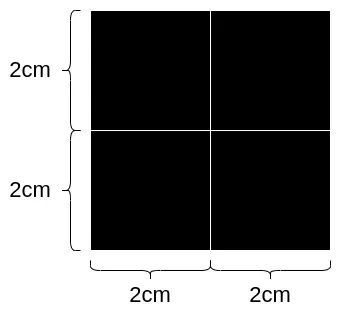
3. You can see that the total area of the square has grown 4 times, generating 4 copies of the original square

And now we can apply our findings to the formula, and calculate the dimension of the square:

You might be thinking: “why would I need to go through all those steps when it is obvious to me that the value of D in the formula 4 = 2^D is 2 and that the dimension of a square is 2? I don’t need logarithms for this…” Well, but what if I asked you to calculate the dimension of a slightly more complicated shape? Say, for example, the Koch Curve? Lets see how we would do that:

1. Draw a Koch Curve

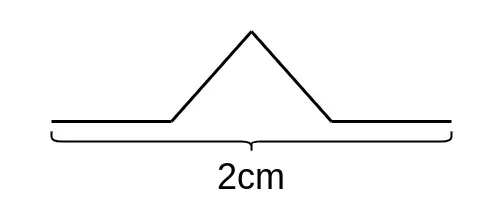
2. Extend its length by 3 and, as we extend its base, we also have to extend its side, to maintain the shape of the fractal.

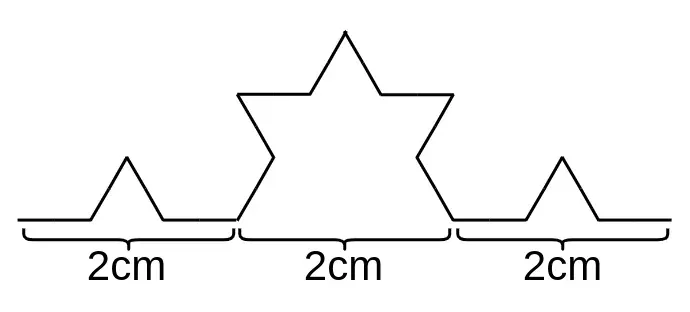
You can see that when we extend the Koch Curve by 3, we end with a total of 4 curves. Plotting this on our formula:

Through this formula we can see that the dimension of the Koch Curve is not and integer, but a fraction: 1.2618. As you saw, for non fractal shapes like the square, the topological dimension and the Hausdorff dimension are the same, but for the fractal shapes, like the Koch Curve, the Hausdorff dimension is greater than the topological dimension.

Later, Mandelbrot considered this definition to be too restrictive and came up with another one: “A fractal is a rough or fragmented geometric shape that can be split into parts, each of which is (at least approximately) a reduced-size copy of the whole.”

By that he meant that a fractal shape is one where the whole of the shape is made up of many smaller copies of itself (property known as self-similarity). The Barnsley Fern is a perfect examples of that:

Each leaf on the Barnsley Fern is a exact copy of the whole, and each leaf is also comprised of smaller leafs that are exact copies of the bigger one. The Mandelbrot Set also contains many copies of itself as you zoom in, infinitely, and the Sierpinski Triangle is also made up of infinite smaller copies of itself.

But that’s enough blabering, on the next post about fractals, we will start doing some cool fractal drawings with Rust and Nannou.

See you there!

Learn More

To learn more about the theory of fractals, don’t miss out on these excellent resources:

Fractals are typically not self-similar (YoutTube video from 3Blue1Brown)

Fractal dimensions. What, why, how to. (YoutTube video from Vu Do Math)

Do fractals exist in nature? (Article on Cosmo Magazine)

Fractal (Wikipedia entry for Fractal)